A. Berpikir Komputasional

1. Mesin Penerjemah Bentuk

Pak Dengklek memiliki sebuah mesin ajaib yang dapat menerjemahkan 26 huruf alfabet (dari A hingga Z) ke 26 bentuk berbeda. Huruf yang sama akan diterjemahkan ke bentuk yang sama, sedangkan huruf yang berbeda akan diterjemahkan ke bentuk yang berbeda.

Untuk menggunakan mesin ini, Pak Dengklek terlebih dahulu menuliskan kata yang ingin diterjemahkan. Kemudian, mesin akan mencetak bentuk-bentuk hasil terjemahan setiap huruf di kata tersebut. Pada akhirnya, bentuk-bentuk ini akan dikumpulkan di dalam sebuah wadah yang dilabeli kata yang diterjemahkan.

Berikut ini merupakan isi dari wadah hasil terjemahan kata "BEBEK" dan "BADAK".

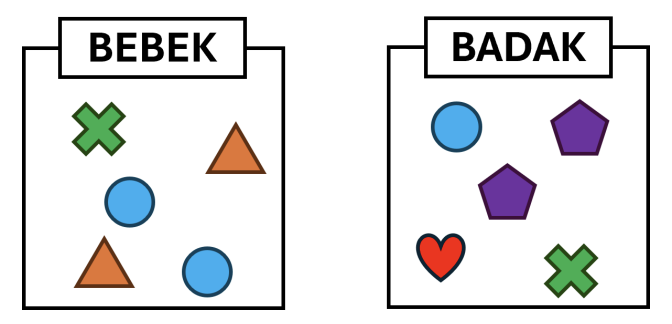
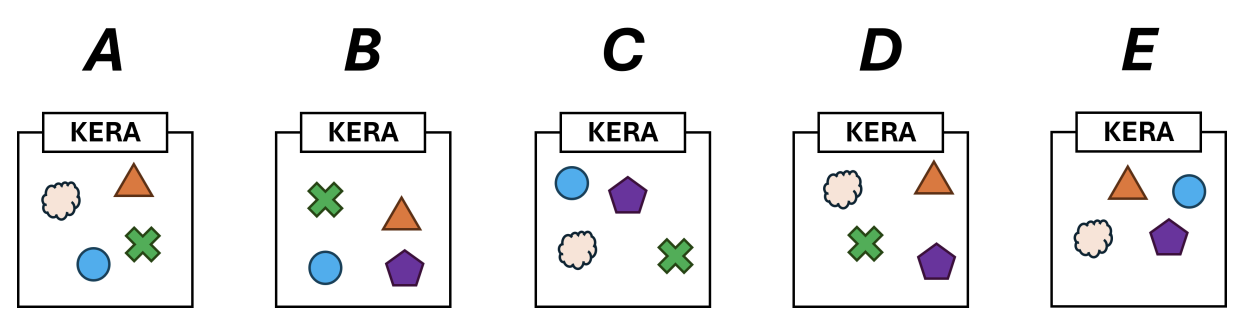
Jika Pak Dengklek ingin menerjemahkan kata "KERA", manakah dari 5 pilihan berikut yang mungkin merupakan isi dari wadah hasil terjemahan?

2. Mengumpulkan Bola dalam Labirin

Pak Dengklek memiliki sebuah labirin yang terdiri dari 100 petak, yang tersusun atas 5 baris dan 20 kolom. Terdapat beberapa bola yang tersebar di beberapa petak. Berikut ini merupakan labirin milik Pak Dengklek tersebut.

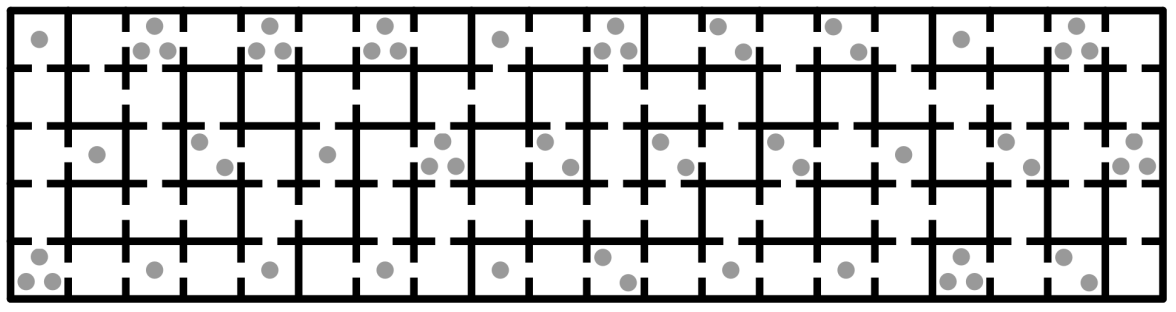
Pak Dengklek ingin meletakkan bebeknya ke salah satu petak kosong. Kemudian, Pak Dengklek ingin bebeknya dapat mengumpulkan sebanyak mungkin bola yang dapat ia temukan. Perhatikan bahwa bebek Pak Dengklek tidak dapat menembus tembok.

Jika Pak Dengklek meletakkan bebeknya secara optimal, berapa maksimal banyak bola yang dapat dikumpulkan oleh bebeknya?

B. Pemecahan Masalah

3–5. Menghitung Subsekuens OSN

Diberikan sebuah string yang hanya terdiri dari huruf-huruf 'O', 'S', dan 'N'; Anda diminta untuk menghitung berapa banyak kemunculan subsekuens "OSN" dari string tersebut.

Secara persisnya, Anda diminta untuk menghitung banyaknya cara memilih huruf 'O', 'S', dan 'N' dari string yang diberikan sehingga huruf 'O' yang dipilih berada sebelum huruf 'S' yang dipilih, dan huruf 'S' yang dipilih berada sebelum huruf 'N' yang dipilih.

Sebagai contoh, ada 2 kemunculan subsekuens "OSN" pada string "SONOSONO", yakni dengan memilih huruf ke-2, 5, dan 7; serta dengan memilih huruf ke-4, 5, dan 7.

Soal 3. Manakah dari 5 pilihan string berikut yang memiliki kemunculan subsekuens "OSN" paling banyak?

• a. "OSNOSN"
• b. "OSSNNN"
• c. "OSSSSSN"
• d. "ONNNSOOON"
• e. "NONONONONON"

Soal 4. Dari seluruh kemungkinan string dengan panjang 9, tuliskan salah satu yang memiliki kemunculan subsekuens "OSN" paling banyak!

Soal 5. Pada string "SONOSONOSONOSONOSONOSONOSONO" (yakni penggabungan 7 kali string "SONO"), berapa kalikah subsekuens "OSN" muncul?

C. Algoritmika

6–8. Merah, Kuning, Hijau

Perhatikan fungsi-fungsi berikut!

Soal 6. Berapakah keluaran dari hijau(123, 456789, 10)?

Soal 7. Asumsikan x, y, dan z adalah bilangan bulat positif tidak lebih dari 100.

Manakah pernyataan yang salah?

• a. Kompleksitas waktu dari fungsi merah(x, y, z) adalah O(y).
• b. Jika y = z, maka fungsi kuning(x, y, z) dijamin selalu mengeluarkan 0.
• c. Ada x dan y sedemikian sehingga merah(x, y, z) = kuning(x, y, z) untuk z apapun.
• d. Keluaran fungsi hijau(x, y, z) selalu dijamin kurang dari z.
• e. Fungsi hijau(x, y, z) dijamin dapat dijalankan dalam 1 detik pada komputer modern.

Soal 8. Asumsikan x, y, dan z adalah bilangan bulat positif tidak lebih dari 100.

Jika baris ke-2 diganti dari int hasil = x % z; menjadi hanya int hasil = x; saja, apakah fungsi hijau(x, y, z) selalu berjalan sebagaimana mestinya sebelum diganti?

Jawablah dengan "YA" atau "TIDAK".